이번 포스팅은 Master Theorem을 처음 배우면서 맛보기(?)를 하면서 끄적인 것이기 때문에 두서가 없습니다.
분할정복에 대해 자세히 알고 싶으신 분은 아래를 참고해주시면 감사하겠습니다.
👉 분할정복
2022.09.28 - [Computer Science/Algorithm] - [Algorithm] 분할정복(1) - Master Theorem과 일반해
[Algorithm] 분할정복(1) - Master Theorem과 일반해
🤔 Divide And Conquer 분할정복이란 일반적으로 주어진 문제를 작은 단위로 분할한 뒤 분할된 문제들을 재귀적으로 해결하여 해당 답을 적절하게 조합하여 큰 문제의 답을 제시하는 알고리즘을 말
2t-hong.tistory.com
2022.09.29 - [Computer Science/Algorithm] - [Algorithm] 분할정복(2) - Multiplication
[Algorithm] 분할정복(2) - Multiplication
🤔 분할정복 분할정복이란 일반적으로 주어진 문제를 작은 단위로 분할한 뒤 분할된 문제들을 재귀적으로 해결하여 해당 답을 적절하게 조합하여 큰 문제의 답을 제시하는 알고리즘을 말합
2t-hong.tistory.com
2022.10.04 - [Computer Science/Algorithm] - [Algorithm] 분할정복(5) - Median of Medians
[Algorithm] 분할정복(5) - Median of Medians
🤔분할정복 분할정복이란 일반적으로 주어진 문제를 작은 단위로 분할한 뒤 분할된 문제들을 재귀적으로 해결하여 해당 답을 적절하게 조합하여 큰 문제의 답을 제시하는 알고리즘을 말합
2t-hong.tistory.com
🤔 Master Theroem
알고리즘 분석에서 Master Theorem(마스터 정리)는 재귀 관계식에서 표현한 알고리즘의 동작 시간을 점근적으로 계산하여 간단하게 계산하는 방법입니다.
앞 시간에 배웠던 Divide-And-Conquer Algorithm에 이어 이해하기 편하도록 특수한 경우에서의 Master Theorem에 대해 배워보겠습니다.
🔎 Divid-And-Conquer 알고리즘의 일반적인 패턴
Input size가 n일 때 Divide-And-Conquer 알고리즘의 일반적인 패턴은 아래와 같습니다.
1. 원래 크기가 $n$인 문제를 size 가 $n/b$ 인 $a$ 개의 subproblem 으로 나누어 줍니다.
2. 각각의 subproblem 을 해결한 뒤 $O( n^d )$ 시간을 사용하여 subproblem 각각의 답을 병합하는 과정을 거칩니다.
위의 과정을 그림으로 나타낸 것입니다.
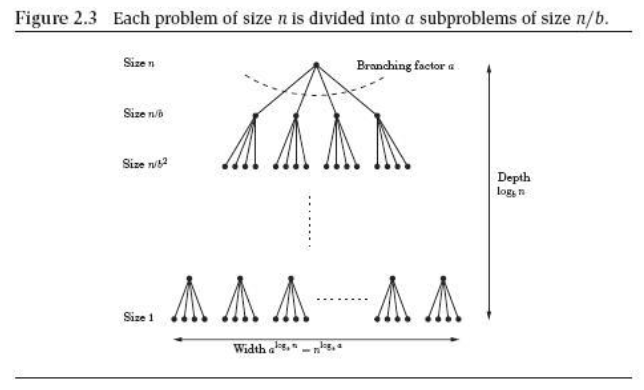
각 node 에 해당하는 문제는 $a$ 개의 subproblem 들로 쪼개지며 input 크기는 $1/b$ 배 줄어듭니다.
따라서 위 recursion tree 의 높이는 는 $log_bn$ 이 됩니다.
또한 $k$ 번째 level 의 node 의 수는 최대 $a^k$ 개이고 각각의 node 에 해당하는 subproblem 의 크기는 $(n/b^k)$ 가 됩니다.
예를 들어 앞에서 배운 Merge Sort Algorithm은 $a = 2$, $b = 2$, $d = 1$의 값을 가집니다.
이와 같은 경우 $a > 0, b > 1, d ≥ 0$에 대해
$$T(n) = aT(n/b) + O(n^d)$$
를 만족하는 점화식을 얻을 수 있습니다.
해당 식의 일반 해 $T(n)$은 아래와 같습니다.

🔎 Master Theorem의 등비수열 형태
위의 과정을 통해 우리는 $a > 0, b > 1, d ≥ 0$에 대해 $T(n) = aT(n/b) + O(n^d)$라는 식을 얻을 수 있었습니다.
해당 식은 점화식으로 등비수열의 summation으로 표현이 가능합니다.
이를 해결하는 과정은 아래와 같습니다

📃Reference
https://ko.wikipedia.org/wiki/%EB%A7%88%EC%8A%A4%ED%84%B0_%EC%A0%95%EB%A6%AC
마스터 정리 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전.
ko.wikipedia.org
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=babobigi&logNo=221005751241
알고리즘) Master Theorem
Master Theorem의 사용 재귀적인 알고리즘을 계산하기 위한 방법이다. 알고리즘의 시간 복잡도를 계산하...
blog.naver.com
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 분할정복(2) - Multiplication (0) | 2022.09.29 |
|---|---|
| [Algorithm] 분할정복(1) - Master Theorem과 일반해 (0) | 2022.09.28 |
| [Algorithm] 알고리즘 기본(2) - Basic Arithmetic (0) | 2022.09.28 |
| [Algorithm] 분할정복 알고리즘 맛보기 (0) | 2022.09.13 |
| [Algorithm] 알고리즘 기본(1) - 알고리즘의 개념과 빅오 표기법 (0) | 2022.09.05 |
![[Algorithm] Master Theorem 맛보기](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbFrtBt%2FbtrL3y4RTTr%2F1HWUtCWMDIdkW30u3rCKJ1%2Fimg.png)