🤔 학습할 내용
이번 시간에는 알고리즘의 이론적 분석과 실험적 분석간의 차이점에 대해 살펴본 후에, Big-Oh notation에 대해 집중적으로 다뤄보도록 하겠습니다. 저번 학기 동안 Computer Structure에서 Big-Oh notation을 다뤘는데 조금 더 자세하게 배워보겠습니다.
🔎 Algorithm
알고리즘이란 어떤 문제를 풀기 위한 유한한 절차와 방법을 말합니다.
여기서 문제는 보통 '수학적으로 엄밀히' 정의된 문제에 한정됩니다.
조금 더 좁은 의미로는 입력값이 주어졌을 때, 수학적으로 엄밀히 정의될 수 있는 답(출력값)을 도출하는 절차와 방법입니다.
알고리즘의 성능을 분석하는 방법에는 실험적 분석과 이론적 분석이 있습니다.
실험적 분석(Experimental analysis)
주어진 알고리즘을 소스코드로 구현한 다음 실제환경에서 동자깃켜 실제 실행 시간을 측정하는 방법입니다.
ex) C언어에서는 clock()이라는 함수를 이용해서 알고리즘의 동작시간을 측정 가능합니다.
실험적 분석의 문제점은 알고리즘을 실제 구현하기까지 시간과 노력이 소모된다는 것입니다.
두 알고리즘의 성능을 비교할 때, 다양한 외부 요인들(하드웨어 사양, 코딩 스타일, 현재 컴퓨터 외부 환경 상태 등)로 인해 정확한 비교가 어렵습니다.
이론적 분석(Theoretical analysis)
알고리즘 수행 시간(=성능)을 실제 구현을 통해서가 아닌, 이론적으로 기술하는 방법입니다.
시간은 보통 입력 사이즈(보통n으로 표기)에 관한 함수로 표현됩니다.
함수의 결과값은 알고리즘을 수행하는데 필요한 기본 연산의 총 횟수를 표현합니다.
사용하는 하드웨어 및 소프트웨어와 무관하게 알고리즘의 성능을 표현 가능합니다.
이론적 분석을 통해 구한 알고리즘 수행 시간을 시간 복잡도(time complexity)라고 합니다.
이론적 분석에서 고려하는 기본 연산들에 대해 알아보겠습니다.
숫자를 변수에 대입하는 경우
함수를 호출, 함수의 결과값을 반환하는 경우
두(작은) 정수 사이의 사칙연산
Array의 Get, Set연산
기타 컴퓨터 하드웨어의 정의된 단일 명령어
etc..(요즘은 컴퓨터의 성능이 매우 좋아져서 다양하다고 하지만 위의 경우만 고려하도록 하겠습니다.)
한 번의 기본 연산을 수행하는데 걸리는 시간은 외부 요인에 따라 다르기 떄문에 일반적으로 정확한 시간은 알 수 없습니다.
하지만 각각의 단일 연산들은 입력 크기와는 무관하다는 것을 알 수 있습니다.
이 경우 이론적으로 연산들은 상수 시간(constant time)이 소모됩니다.
🔎 Big-Oh Notation
Big-Oh notation (Big-Oh 표기법)에 대해 알아보겠습니다.
이론적 분석에서는 걸리는 시간을 표현한 함수 자체보다 입력 사이즈에 비례해서 해당 함수가 어느 정도로 증가하는가에 더 관심이 많습니다.
앞선 constant time 연산들은 입력 사이즈와 무관할 뿐더러 함수가 증가하는 속도와도 거의 무관합니다.
예를 들어 컴퓨터 1보다 모든 기본 연산들이 10배 빠른 컴퓨터 2가 있다고 했을 때 실제 성능에서도 복잡한 알고리즘일수록 기본 연산들의 속도차이는 거의 무의미해집니다.
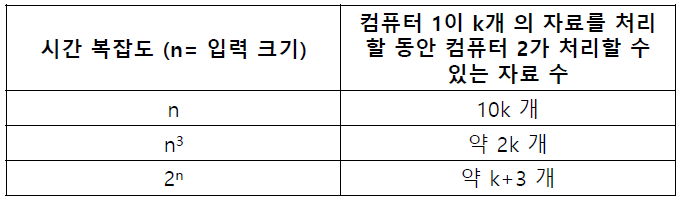
시간복잡도가 n이라면 n시간동안 컴퓨터 1이 K개의 자료를 처리할 때, 컴퓨터 2는 10K개의 자료를 처리할 수 있습니다.
하지만 시간복잡도가 n³이라면 컴퓨터 1이 K개의 자료를 처리할 때 컴퓨터 2는 2.~K개의 자료를 처리합니다.
기본 연산들이 10배 빠르다고 해도 복잡한 알고리즘에서는 속도차이가 무의해짐을 나타냅니다.
Big-Oh Notation의 정의
Big-Oh Notation의 정의는 아래와 같습니다.

수학적 기호를 활용하여 아래와 같이 표현할 수 있습니다.

즉 조건을 만족하는 $c$와 $n_0$을 찾으면 Big-Oh Notation을 사용하여 함수를 나타낼 수 있습니다.
예시 문제를 풀어보도록 하겠습니다.
먼저 상수함수 $f(n) = 30$를 Big-Oh Notation으로 표기해보겠습니다.
상수함수는 $n$과 관계없이 항상 일정한 값을 가지고 있으므로 30보다 큰 $c$가 존재한다면 이를 만족합니다.
Big-Oh Notation에서는 이를 $f(n) = O(g(n))$로 나타냅니다.
1차함수인 $f(n) = 3n + 1000$의 Big-Oh Notation을 표기하기위해 정의를 만족하는 $c$와 $n0$를 찾아보겠습니다.
$c = 100$이라 하면 $f(n) = 3n + 1000 ≤ 100n + 1000$이므로 $n_0 > 1000$ 일떄 정의를 만족합니다.
최고차항이 $d$인 다항식은

에 따라 $f(n) = O(n^d)$ 라는 점을 쉽게 증명 가능합니다.
추가 예시를 풀어보시면 도움이 될 것 같습니다.
✏️추가 예제
1. $f(n) = 30$일 때, f(n)의 시간 복잡도를 Big-Oh Notation으로 표기하시오.
2. $f(n) = 3n + 1000$일 때, f(n)의 시간 복잡도를 Big-Oh Notation으로 표기하시오.
3. $f(n) = 3n^2 - 4n + 2$일 때, f(n)의 시간 복잡도를 Big-Oh Notation으로 표기하시오.
4. $f(n) = 100n^3 + 10nlogn + 2$일 때, f(n)의 시간 복잡도를 Big-Oh Notation으로 표기하시오.
5. $f(n) = logn + 2loglogn - 3$일 때, f(n)의 시간 복잡도를 Big-Oh Notation으로 표기하시오.
6. $f(n) = 2^n+2$일 때, f(n)의 시간 복잡도를 Big-Oh Notation으로 표기하시오.
참고
$f(n) = n!$일 때, f(n)의 시간 복잡도는 $O(n^n) 입니다.
어떤 함수를 Big-Oh notation으로 표현하는데 있어서 몇 가지 규칙이 있습니다.
1. 함수의 각 term 의 coefficient 는 생략 가능 (ex : $13n^2 = O(n^2)$).
2. $a > b$ 인 경우 $n^a$ 와 $n^b$ term 이 같이 있으면 $na$ term 만 남길 수 있음.
(이 경우 $na$ dominates $nb$라 함) ex:$ f(n) = n⁴ + n³ = O(n⁴)$
3. 어떠한 exponential (지수함수) term도 polynomial term 을 dominate 함.
(ex : $1.00001^n$ dominates $n^100000000)$)
4. 어떠한 polynomial term 도 logarithm (로그 함수) term 을 dominate 함.
(ex : $n $dominates $log_n100000000$)
Notation Ω (Omega) 와 ϴ (Theta) o(Little-Oh)
$f(n), g(n)$에 대해 $f(n) = O(g(n))$를 만족하면 $g(n) = Ω (f(n))$이라고 나타낼 수 있습니다.
수학적 기호로 나타내면 아래와 같습니다.
$∃ c, n_0 > 0$ such that $∀ n > n_0, g(n) ≥ c ⋅ f(n)$
$f(n) = O(g(n))$ 임과 동시에 $g(n) = O(f(n))$ 이면 $f = ϴ(g(n))$ 그리고 $g = ϴ(f(n))$ 이라고 나타낼 수 있습니다.
수학적 기호로 나타내면 아래와 같습니다.
$ ∃ c_1, c_2, n_0 > 0$ such that $ ∀n > n_0, c _1⋅ f(n) ≤ g(n) ≤ c_2 ⋅ f(n)$
$f(n), g(n)$ 에 대해 아래 조건을 만족하면 $f(n) = o(g(n))$ 이라고 나타낼 수 있습니다.
$∀ c, ∃ n_0 > 0$ such that $∀n ≤ n_0, f(n) ≤ c ⋅ g(n)$
실제 코드나 알고리즘의 이론적인 수행 시간을 분석할 때는 알고리즘을 구현한 코드에서는 1) 변수의 대입 횟수, 2) 반복문 (for, while…) 에서의 반복 횟수, 3) 함수의 호출 및 리턴 수 등 기본 연산들의 수행 횟수가 입력 크기에 비례하여 어느 정도로 커지는지 파악하는 것이 중요합니다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 분할정복(2) - Multiplication (0) | 2022.09.29 |
|---|---|
| [Algorithm] 분할정복(1) - Master Theorem과 일반해 (0) | 2022.09.28 |
| [Algorithm] 알고리즘 기본(2) - Basic Arithmetic (0) | 2022.09.28 |
| [Algorithm] Master Theorem 맛보기 (0) | 2022.09.14 |
| [Algorithm] 분할정복 알고리즘 맛보기 (0) | 2022.09.13 |
![[Algorithm] 알고리즘 기본(1) - 알고리즘의 개념과 빅오 표기법](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fbixs0h%2FbtrLsqFVZ03%2FkKeJrCASub9H3XYMjvR4CK%2Fimg.png)