🤔 Dynamic Programming
다이나믹 프로그래밍이란 큰 문제를 작은문제로 나누어 문제를 해결하는 것을 말합니다.
다이나믹 프로그래밍 알고리즘을 이용하는 다양한 알고리즘에 대해 알아보겠습니다.
이번 포스팅에서는 LIS문제를 해결하기 위해 Dynamic Programming을 사용하여 해결하는 과정을 정리했습니다.
🔎 LIS(Longest Increasing Subsequence)
✍️Subsequence
길이 n 인 sequence (ordered list) $S = a_1, a_2, …, a_n$ 이 주어졌을 때, sequence $S’ = a_{i1}, a_{i2}, .., a_{ik} 가 1≤ i1 < i2 < … < ik ≤n$ 를 만족할 경우 $S’$ 을 $S$의 subsequence 라고 합니다.

또한 $a_1 < a_2 < …< a_n$ 일 때, sequence S 는 increasing sequence라고 할 수 있습니다.
✍️ LIS
LIS문제를 해결하기 위해 DP를 사용합니다.
이전 포스트에서 말한 해결 과정을 통해 LIS를 구해보겠습니다.
1. 문제를 정확하게 정의한다.
S를 $a_1, a_2, ..., a_n$로 구성된 Sequence라고 하겠습니다.
Problem : S에서 가장 긴 increasing subsequence의 길이 구하기.
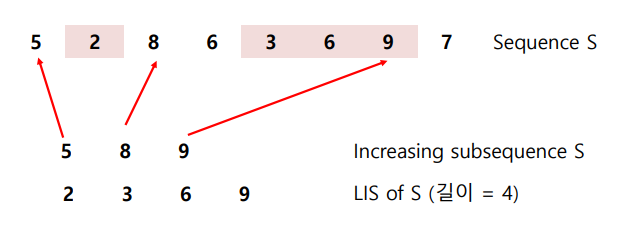
2. 정의된 문제에 대한 subproblem 을 정의한 뒤 subproblem 을 이용한 recurrence relation 을 세운다.
L(i) = S의 첫 i개의 element $a_1, a_2, … , a_i$ 로 이루어진 sequence 에서 LIS 의 길이라고 두자.
L(i)를 L(1), L(2), …, L(i-1) 로 나타낼 수 있을 지를 확인합니다.
L(i)를 첫 i개의 element $a_1, a_2, … , a_i$ 로 이루어진 sequence 에서 $a_i$ 로 끝나는increasing subsequence 들 중 가장 긴 subsequence의 길이라 하자
L(i)를 위와 같이 정의하면 다음과 같은 recurrence relation이 만족한다는 것을 알 수 있습니다.
$$L(i) = 1 + max_{j < i, a_j < a_i}L(j)$$
또한 이 경우 S의 LIS의 길이는 $max^n_{i=1}L(i)$가 됩니다.
위의 recurrence relation에서 중요한 포인트는 "$a_i$로 끝나는"입니다.
이를 통해 memoization을 실행 할 수 있습니다.
👉 LIS 수도코드
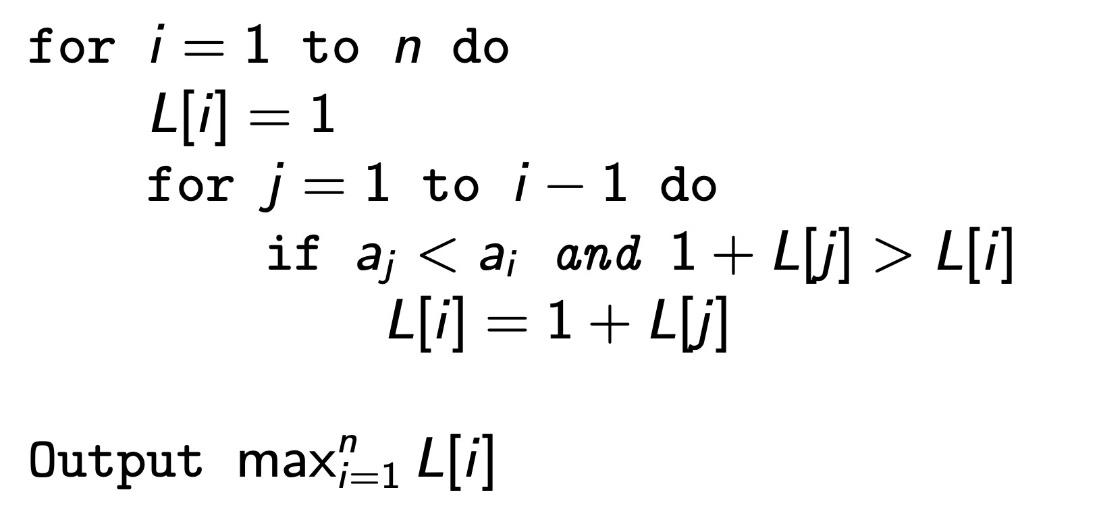
Subproblem $L(i)$를 구하기 위해서 $L(1), ... , L(i-1)$의 값을 알아야 하므로 $L(1)$부터 왼쪽 부터 해결해야 합니다.
3. Memoizaion 을 이용하여 recurrence relation 계산합니다.
- 중간 결과물들을 저장할 data structure를 고릅니다. (보통 n 차원 array 사용.)
→ 1차원 array를 사용하면 $L(i)$값을 저장하여 사용할 수 있습니다.
- Subproblem 들 간의 dependency를 확인합니다. (예 : $ 을 구하려면 어떤 subproblem의 답들을 계산해 놓아야 하는가?)
→ $L(i)$는 $L(j)$의 값에 의존합니다.
- Dependency 에 기반하여 subproblem 들의 답을 구하는 순서를 정합니다.
이를 예제를 통해 이해해보겠습니다.



LIS의 길이 = L(7) = L(8) = 4
- 실제 LIS 는 $L(i) = L(j)+1$ 로 업데이트 할 때마다 $a_i$ 로 끝나는 LIS 의 직전 element 가 $a_j$라는 사실을 따로 array 로 저장합니다.(위 예시의 pre)
이 경우 S의 LIS 가 max 에서 끝난다면 $S_max$ 로부터 pre 를 따라 역으로 추적하면 됩니다.
4. Time complexity를 분석하고 알고리즘을 작성합니다.
$L(i)$를 계산할 때 조건에 맞는 $L(j)$ 검색 → $O(i - 1)$
즉, i번째 element를 분석할 때 마다 i-1번의 연산을 진행한다는 것이므로 총 시간복잡도 → $O(1 + 2 + ... + n-1) = O(n^2)$
모든 $L(i)$ 계산 뒤, 해당 값이 가장 큰 i를 찾습니다. → $O(n)$
총 시간복잡도 $O(n^2)$
참고로 LIS를 구하는 가장 빠른 알고리즘은 $O(nlogn)$ 입니다.
✍️ LIS를 구하는 다른 방법
DAG를 이용하여 LIS를 구하는 방법이 있습니다.
이는 아래의 링크를 참고하시길 바랍니다.
https://www.geeksforgeeks.org/find-longest-path-directed-acyclic-graph/
Longest Path in a Directed Acyclic Graph - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
다음 포스팅에서는 Edit Distance 알고리즘에 대해 알아보도록 하겠습니다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] Dynamic Programming(4) - 벨만포드(Bellman-Ford) (0) | 2022.11.19 |
|---|---|
| [Algorithm] Dynamic Programming(3) - Edit Distance(편집거리) (0) | 2022.11.19 |
| [Algorithm] Dynamic Programming(1) - Warm Up (0) | 2022.11.15 |
| [Algorithm] 분할정복(4) - Selection (0) | 2022.10.20 |
| [Algorithm] 분할정복(3) - Matrix Multiplication (0) | 2022.10.20 |
![[Algorithm] Dynamic Programming(2) - LIS(Longest Increasing Subsequence)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcZi4Pm%2FbtrRvbPAnGM%2FfgnLKL5FIf7YuhLPHZBkA1%2Fimg.png)