[ML] Ensemble Method(4) - Gradient Boost
🤔 Ensemble Method
통계학과 기계 학습에서 앙상블 학습법은 학습 알고리즘들을 따로 쓰는 경우에 비해 더 좋은 예측 성능을 얻기 위해 다수의 학습 알고리즘을 사용하는 방법 입니다.
통계 역학에서의 통계적 앙상블과 달리 기계 학습에서의 앙상블은 대체 모델들의 단단한 유한 집합을 가리키지만, 일반적으로 그러한 대체 모델 사이에 훨씬 더 유연한 구조를 허용합니다.
이전 포스팅에서 배운 Boosting 알고리즘을 발전시킨 Gradient Boost에 대해 알아보도록 하겠습니다.
🔎 Gradient Boost
Gradient Boost를 알기 위해 Gradient의 개념을 알아야 합니다.
Gradient는 기울기 즉 1차 미분 값이라는 뜻입니다.
나중에 배우게 될 NN과 딥러닝알고리즘이 결국에는 기울기 기반으로 학습을 진행합니다.
Gradient Boost는 이를 Boosting에 적용했다고 할 수 있습니다.
✍ 경사하강법(Gradient Descent)
아래와 같은 $J(a)$라는 목적 함수가 존재한다고 하겠습니다.
이때 $a_k$는 모델의 solution이자 weight, parameter을 의미합니다.

이때 $a_k$를 sequential 하게 업데이트를 적용하는데 아래와 같은 방법을 사용합니다.

그래프를 살펴보았을 때 목적함수는 $a$에 대한 함수입니다.
이때 목적함수는 Loss Function, Cost Function을 의미합니다.
그러므로 우리는 해당 함수의 최소값을 찾으려고 노력해야 합니다. ($min(J(a))$을 찾는다.)
최소화를 위해서 그림의 경우에는 한 번만 미분을 하면 되지만 실제 LSM(Least Square Method)를 사용하지 못한다고 가정하겠습니다.(한 번의 미분으로 해결이 안 된다고 가정)
이때 우리는 $a_k$를 왼쪽으로 조금 이동을 하여 더 작은 값을 찾을 수 있습니다.
해당 과정을 반복하다가 0이 될 때 Optimal한 값을 찾을 수 있습니다.
쉽게 비유를 하자면 등산을 할 때 하산을 하기 위해서 우리는 경사면의 반대로 이동해야 합니다.
이때 평지를 찾게 된다면 이를 Local Optimum이라고 할 수 있습니다.
즉, 미분을 한 뒤 기울기의 반대방향으로 움직여야 한다는 뜻입니다.
이를 수식으로 나타내면 아래의 수식과 같습니다.

이때 Global Optimum 은 아니더라도 Local Optimum에 도달할 수 있게 됩니다.
해당 알고리즘을 이용한 것이 Gradient Boost 입니다.
Example
예시를 통해 Gradient Boost를 알아보겠습니다.
Regression에 Gradient Boost를 적용한 예제를 살펴보겠습니다.
해당 알고리즘은 아래와 같은 순서로 이뤄집니다.
1. y값에 해당하는 값들의 평균을 통해 Initial Guess를 진행합니다.
2. 중간과정의 잔차($y - \hat{y}$)를 계산한 뒤 잔차를 맞추는 Tree를 구성합니다. 이때 Tree는 Underfit 모델을 사용하기 때문에 2~4의 depth를 가집니다. 이때 비슷한 잔차를 가지는 데이터를 묶어 Leaf Node로 둔 다음 해당 값들의 잔차의 평균을 구합니다.(아래의 그림의 경우 임의로 예측값을 삽입했습니다)
3. 사용자가 설정한 하이퍼 파라미터인 $\alpha$를 해당 Tree의 값과 곱한 값을 이전 Tree에 더하여 다음 $\hat{y}$를 설정합니다.
4. 2, 3을 반복으로 진행합니다.
5. 4와 동일
6. 더 이상의 변화가 없다고 느껴질 때가지 위의 과정을 반복합니다.
이를 표와 Tree를 통해 나타내면 아래와 같습니다.
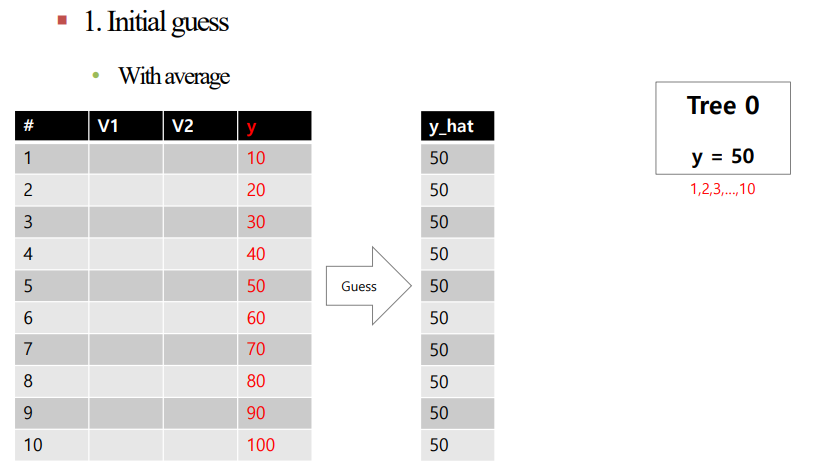
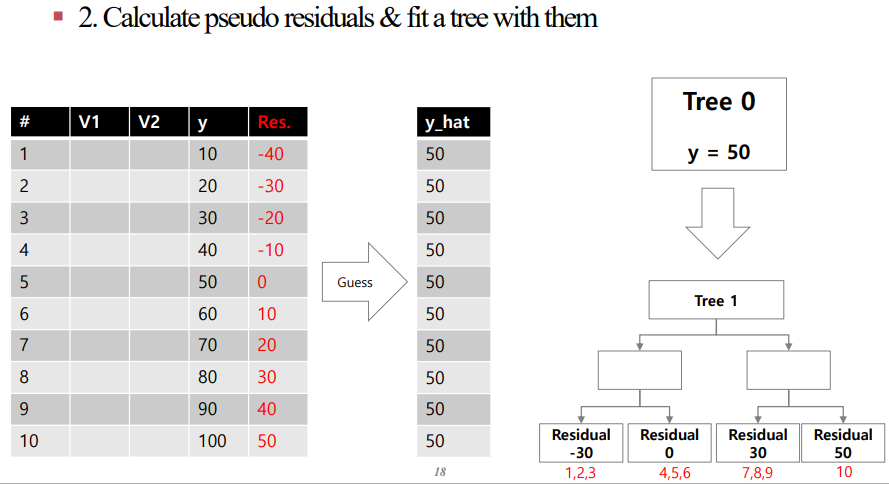
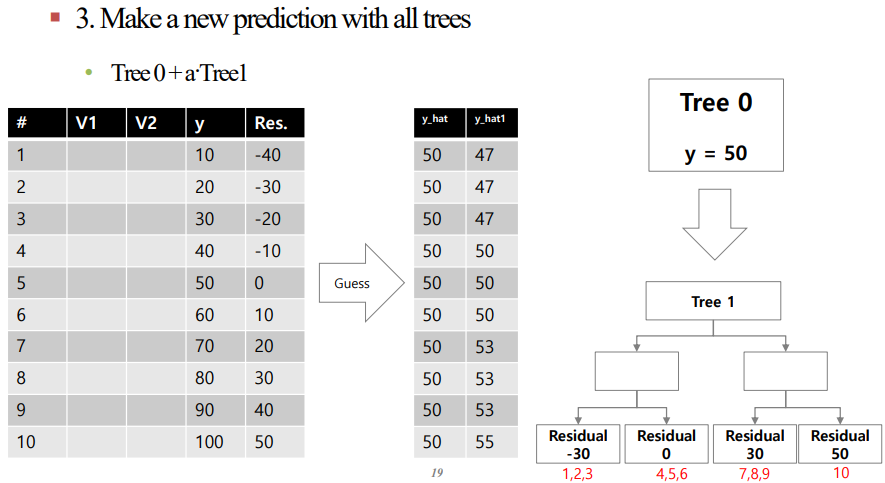
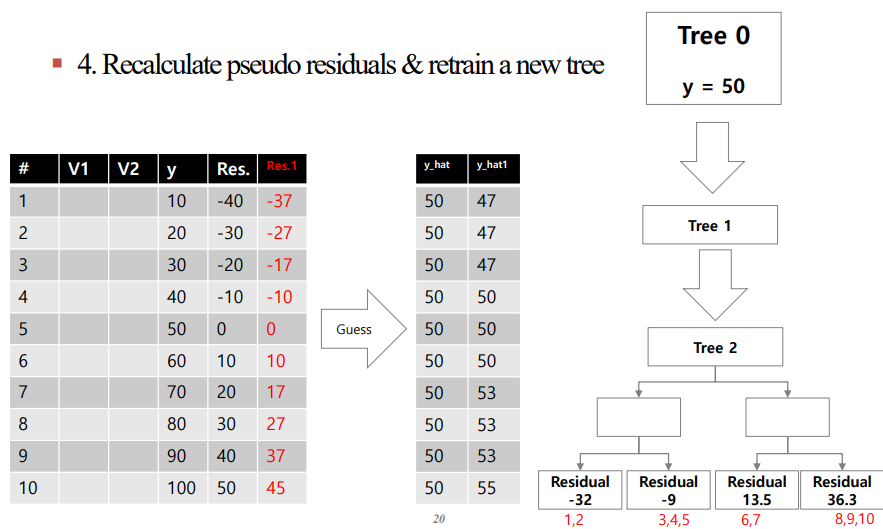
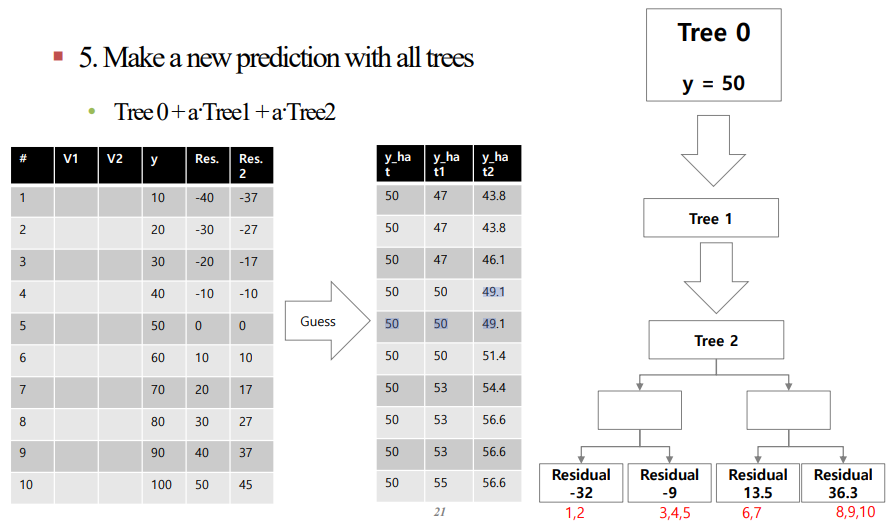
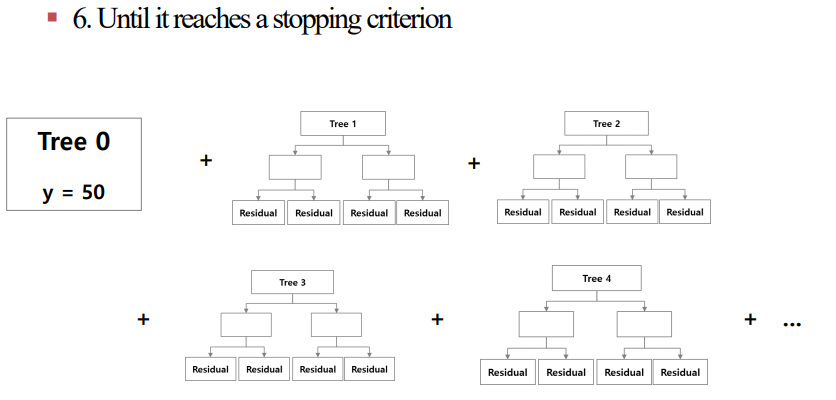
결론적으로 residual을 맞추는 Tree를 만드는 것이 최종 목적입니다.
해당 Residual값을 점점 감소시켜서 줄여라!
✍ Gradient Tree Boosting Algorithm for Regression
Gradient Tree Boosting Algorithm을 살펴보겠습니다.

전체적으로 보았을 때 initialize에서 평균을 삽입하라는 뜻입니다.
이후 MSE를 생각하여 L은 아래와 같다고 하겠습니다.

$r_{iM}$에 기울기 감소(Gradient Descent)값을 입력합니다.
위의 수식을 미분하면 아래와 같게 됩니다.

이를 정리하면 아래와 같습니다.

즉, $y_i - f(x_i)$는 잔차를 의미합니다.
Residual을 맞추는 Tree를 생성하는 것이 우리의 목적이기 때문에 Loss Function의 Gradient의 역방향으로 이동하여 이를 맞추겠다는 것입니다.
결국 "Residual을 맞추는 Tree를 만든다 = Gradient Descent를 실행한다"를 의미하는 것을 알 수 있습니다.
위의 알고리즘에서 $R_{jm}$에서 $j$는 Leaf Node Number을 의미하는데, Leaf Node 각각 평균을 설정해 줬습니다.
이때 각각의 terminal region이기 때문에 Leaf Node를 의미합니다.
이를 최소화 하는 감마 값을 찾아서 이를 $r_Pjm}$에 삽입합니다.
해당 과정에서의 Loss Function은 아래와 같습니다.

이를 미분했을 때 0이 되는 값을 찾으면 $\sum\gamma = \frac{\sum(y_i - f_{m-1}(x_i))}{1}$일 때 만족합니다.
최종적으로 $\gamma = \frac{\sum(y_i - f_{m-1}(x_i))}{n}$일 때를 의미합니다.
이것이 의미하는것이 각 Leaf Node의 값은 평균이라는 것과 동일합니다.
다음 솔루션에서 해당 감마의 값을 더해줍니다.
해당 솔루션들을 모두 더한 값이 $\hat{f(x)} = f_M(x)$을 의미합니다.
정리하자면 위와 같이 Gradient Descent를 Boosting에 적용하는 방법이 Gradient Boost입니다.
✍ Gradient Tree Boosting Algorithm for Classification
Classification 의 경우 나머지는 모두 동일하지만 Loss Function이 다릅니다.
Logistic Regression에서 학습했던 내용 중 Odds, Log Odds에 대한 개념을 먼저 이해해야 합니다.

짧게 설명하자면 해당 함수는 Logistic Sigmoid 함수라는 것을 알고 가시면 됩니다.
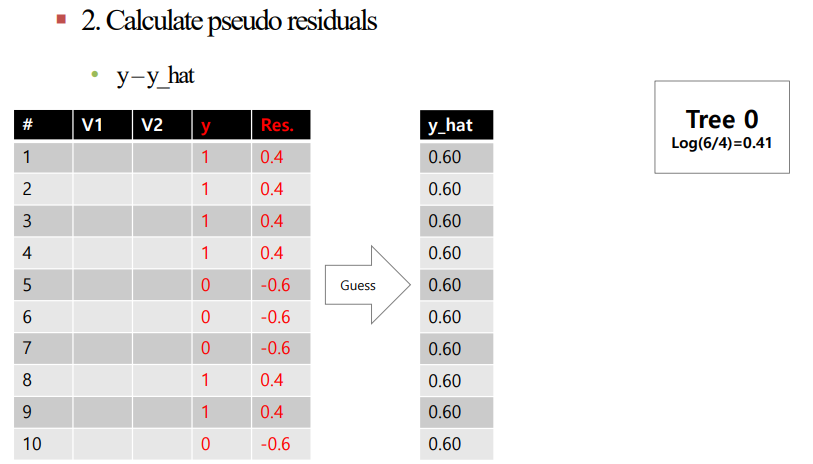
Refression에서와 같이 이를 진행한다면 아래의 예시와 같습니다.
Example
주의해야 할 것은 $\hat{y}$값을 직접 건드렸던 Regression과 달리, Classification에서는 $Log(odds)$를 누적해야 한다는 것입니다.
4번 과정에서 Tree0의 $Log(odds) = 0.41$이고 Tree1의 첫 번째 Leaf Node의 값이 1.66이므로 $0.41 + 0.1\times1.66 = 0.4266$을 얻을 수 있습니다.
이를 다시 Probability로 변환하면 0.61이라는 값을 얻을 수 있습니다.



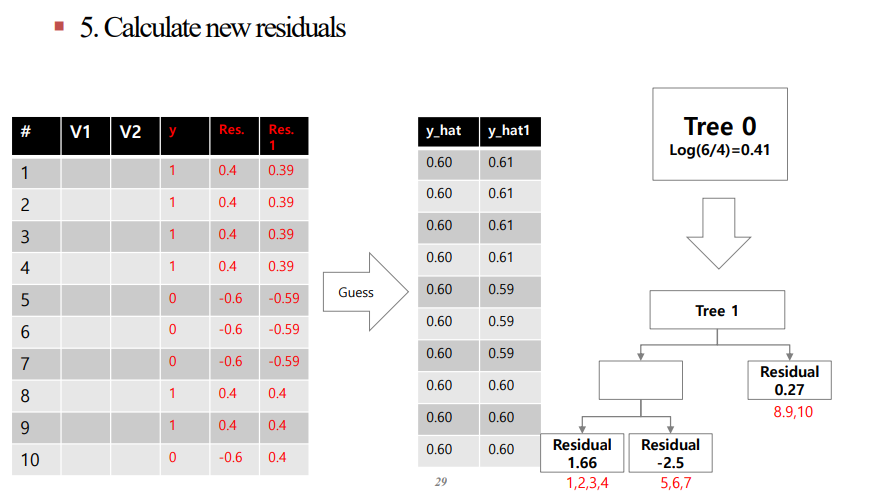

알고리즘을 살표보면 아래와 같습니다.

앞에서 살펴본 Gradient Tree Boosting Algorithm for Regression과 Loss Function을 제외하고 동일합니다.
Regression의 경우 Loss Function을 MSE로 봐도 무방했기 때문에 깔끔하게 전개가 됐지만, Classification의 경우 MSE와 같은 미분 가능한 Loss Function을 만들기 어려워서 위와 같은 복잡한 알고리즘을 사용합니다.
위의 알고리즘은 베르누이 분포로 부터 생성되는데 아래와 같은 과정을 거칩니다.

우리는 Loss Function계산하여 Gradient Descent를 진행해야 하는데 Loss Function이 낮을 수록 좋기 때문에 높을 수록 좋은 Likelihood를 negative하게 계산합니다.
최종적으로 Negative Log Likelihood를 사용합니다.
해당 식을 전개하면 아래와 같습니다.

결론식으로 아래와 같은 수식을 얻을 수 있습니다.

해당 식을 최소화 하는 값을 찾는 것이 위의 알고리즘을 해결하는 방법입니다.
위의 알고리즘을 해결하다보면 $ y_i - p_i$라는 중간 잔차를 얻을 수 있습니다.
일반 Regression과의 가장 큰 차이점은 개별 노드의 Output을 Regression에서는 평균을 통해 구했는데, Classification의 경우 아래와 같은값을 Leaf의 Output 값으로 사용합니다.

증명은 생략하도록 하고 가장 중요했던 것을 강조하고 마치도록 하겠습니다.
목적함수인 $f(x_i)$는 $Log(odds)$를 의미하며 이는 트리의 Leaf Node의 output을 의마한다는 것입니다.
증명이 궁금하신 분은 아래의 링크를 참고하시기 바랍니다.
✍ Gradient Boost 특징
Gradient Boost의 경우 weak learner들의 Leaf Node 개수는 일반적으로 $2^3 ~ 2^5$이며 depth는 3~5정도가 됩니다.
즉, Underfit한 모델을 사용한다는 것입니다.
Tree의 경우 일반적으로 100정도의 Iteration을 가집니다.
또한 Learning Rate를 사용하여 Log(odds)값의 비율을 조정해줍니다.
다음 포스팅에서는 XGBoost 기법에 대해 알아보도록 하겠습니다.
🔎 Reference
https://analysisbugs.tistory.com/225
[Machine Learning] Gradient Boosting (Classification)
본 포스팅은 STATQUEST 유튜브 채널을 참고하였습니다. 위의 데이터에 대해서 3가지 input attribute로 Love troll 2를 예측하고자 한다. Classification Task 이므로 오차 함수를 Cross Entropy로 정의한다. Step 1) ▶
analysisbugs.tistory.com